Para ilustrar este concepto, consideremos el siguiente ejemplo práctico:
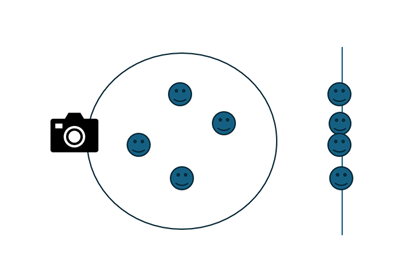
Supongamos que nos encontramos en una fiesta familiar y nos toca ser el fotógrafo. Imaginemos que nuestros familiares están dispersos en el espacio de la fiesta. Si tomamos una fotografía desde un ángulo inadecuado, es probable que no todos los familiares aparezcan en la imagen. Esto se puede ver en el siguiente gráfico:
El análisis de componentes principales (PCA) se centra en la identificación de una rotación de los datos alrededor de un eje que maximice la conservación de la varianza. Esto implica orientar el conjunto de datos de manera que se observe la mayor cantidad de "puntos" o variabilidad entre ellos. La varianza es clave en PCA porque nos permite discernir la información más significativa contenida en los datos.
Para comprender a fondo el PCA, es esencial familiarizarse con algunos conceptos estadísticos fundamentales que subyacen en este método analítico.
Conceptos Clave en el Análisis de Componentes Principales (PCA):
Promedio (Media):
Número que no es el promedio:
Número que si es el promedio:
Varianza:
Ejemplo de la información que nos brinda la Varianza:
A. 4, 4, 4, 4
B. 1, 1, 7, 7
Ambas aulas tienen un promedio de 4, pero sus distribuciones son notablemente distintas. El aula A tiene una varianza de 0, indicando homogeneidad total en las notas. Por otro lado, el aula B, con una varianza de 9, muestra una alta heterogeneidad. Esto ejemplifica cómo la varianza puede revelar diferencias en la dispersión de los datos que el promedio solo no puede.
Normalización:
Este proceso ajusta los valores numéricos a una escala común sin distorsionar diferencias en los rangos de valores o perder información, similar a estandarizar ingredientes en una receta para que cada componente combine de manera equilibrada.
Standardization (Estandarización): También conocida como Z-score normalization. Este método reescala los datos para que tengan una media (promedio) de 0 y una desviación estándar de 1. La fórmula es:
Donde µ es la media del conjunto de datos, y o la desviación estándar.
Covarianza:
La covarianza mide la relación lineal entre dos variables. Un valor positivo indica que ambas variables tienden a incrementar juntas, mientras que un valor negativo sugiere que se mueven en direcciones opuestas. La función .cov() en Python permite calcular la covarianza entre dos conjuntos de datos.
Para esta interpretación supongamos que tenemos 2 variables ya normalizadas. Si observamos las variables de la siguiente manera:

Acá podemos ver que la varianza para los dos conjuntos de datos es la misma tanto del plano X, como del plano Y. para determinar la covarianza lo que hacemos es usar las coordenadas del plano cartesiano, es decir hacemos la suma del producto de coordenadas.
a) b)
(-1,-1) = 1 (-1,1) = -1
(0,0) = 0 (0,0) = 0
(1,1) = 1 (1,-1) = -1
Figura A covarianza de 2, Figura B covarianza de -2. De esta forma podemos diferenciar la dirección de nuestros datos quedando la covarianza de la siguiente manera:
Una vez que tengamos la matriz de covarianza podemos sacar de esta los vectores y los valores propios Los vectores propios nos darán las direcciones de los nuevos ejes (componentes principales), mientras que los valores propios nos dirán cuánta varianza hay en los datos a lo largo de esos ejes. A continuación, realizaremos un ejemplo sencillo de cómo se obtienen.
Imaginemos que tenemos un conjunto de datos con dos variables Y , X y vamos a calcular su matriz de covarianza y sus vectores y valores propios.
Para encontrar los valores propios (λ) y los vectores propios (v), necesitamos resolver la ecuación característica:
donde:
𝐴 es la matriz de covarianza.
𝜆 es un valor propio.
𝐼 es la matriz identidad del mismo tamaño que
det denota el determinante de la matriz.
Si calculamos la matriz de covarianza de nuestros datos seria la siguiente:
matriz de identidad:
Paso 2: Calcular el Determinante y Resolver para 𝜆
El determinante de 𝐴−𝜆𝐼 es:
Resolviendo la siguiente ecuación:
nos dará los valores propios.
Esta es una ecuación cuadrática en términos de 𝜆. Los valores propios λ que satisfacen esta ecuación son críticos porque indican las "direcciones" en las que la variación de los datos es máxima (en el caso del primer componente principal) y decreciente en importancia con los siguientes componentes principales.
Para resolver esta ecuación cuadrática, podemos utilizar la fórmula cuadrática:
Donde a=1, b=−3.333, y c=0.75. Sustituyendo estos valores en la fórmula, obtenemos:
Las soluciones a esta ecuación son los valores propios de la matriz de covarianza. Estos valores nos indican cuánta varianza hay en cada una de las direcciones (vectores propios) identificadas por PCA, y seleccionamos componentes basados en estos valores para maximizar la varianza retenida al reducir la dimensionalidad.
Finalmente, calcularíamos los vectores propios correspondientes a cada valor propio resolviendo (A−λI)v=0 para cada λ. Estos vectores propios son los que realmente forman los ejes o direcciones a lo largo de los cuales se proyectan los datos en el espacio de menor dimensionalidad.
Veámoslo con un ejemplo de dos variables una vez tenemos los vectores y valores propios estos proyectados en un gráfico bidimensional quedaría de la siguiente manera
No tenemos que observar la magnitud (longitud) de los vectores lo que en realidad importa es la dirección en la que apuntan los vectores. Esto nos dará la dirección la cual proyectar nuestros datos conservará la mayor cantidad de información. La operación que realizamos para proyectar nuestros datos se conoce como producto punto o producto escalar, entre cada fila del conjunto de datos y el vector PC1. Esto se hace para cada observación datos, transformándola a la nueva base definida por el vector del componente principal.
¿Qué es el Producto Punto?
El producto punto entre dos vectores es una operación que resulta en un único número (escalar). Matemáticamente, el producto punto de dos vectores a y b de longitud n se define como:a⋅b=a1×b1+a2×b2+…+an×bn
ejemplifiquemos con el siguiente vector:
Este vector es solo de un componente principal. el componente principal con que mayor varianza explica entonces ¿cómo sería el producto punto entre este vector y mis datos? imaginemos que tenemos el siguiente DF.
Ahora veámoslo con una representación más matemática:
Proyectar el DataFrame en los vectores propios haciendo el producto punto entre D(dataframe) y el vector propio del primer componente:
La multiplicación de matrices aquí calcula la combinación lineal de las columnas de D (variables) ponderada por los elementos de Vpc1 (vector propio del primer componente). El resultado es una nueva matriz donde cada registro es la proyección de los datos en el componente principal 1.
Ejemplo de Cálculo para la Proyección sobre PC1
Dada la
primera fila del DataFrame con las coordenadas [17.042443, 27.017066], queremos
calcular su proyección sobre el primer componente principal (PC1).
PC1 = [-0.99245292,
0.12262626]
Para
calcular la proyección, realizamos el producto punto entre las coordenadas de
la primera fila y el vector PC1:
Primera Fila Proyectada sobre PC1 = (17.042443 *-0.99245292) +
(27.017066 * 0.12262626)
Proyección = (-16.90638856) + (3.31324861)
Proyección = -13.59313995
Este valor
representa la proyección de la primera fila sobre el componente principal PC1.
Este resultado es un número único, porque la proyección es sobre un único componente principal (PC1) reduce la dimensión de los datos a una sola medida por observación, que indica la "coordenada" de esa observación a lo largo del eje definido por PC1.
Conclusión
Este valor, -13.59313995 , representa cómo la primera observación se proyecta en el primer componente principal. Este componente, como recordamos, es el que captura la mayor parte de la varianza, lo cual es útil para análisis donde interesan los patrones principales de variabilidad dentro de los datos.
Si hacemos la proyección de cada registro por los dos vectores realizaríamos la siguiente rotación en nuestros datos:

dado que estamos solo haciendo una proyección la visualización correcta seria la siguiente:
Aplicación
Práctica y Conclusión
El PCA es
como realizar un "giro" en nuestros datos que maximiza la varianza
conservada, similar a cómo podríamos ajustar una fotografía para enfocar mejor
a un grupo de familiares. Este método es invaluable en grandes conjuntos de
datos, facilitando la estimación eficiente de cuántos componentes principales
son necesarios para captar la mayor parte de la varianza.
Es
fundamental tener en cuenta el dominio específico de los datos y los objetivos
del análisis al aplicar PCA. Este proceso no solo reduce la dimensionalidad,
sino que también mejora la eficiencia computacional durante la modelización y
ayuda a entender mejor cuánto contribuye cada variable a los componentes
principales. Esta capacidad de discernir qué variables son más informativas
respecto a la varianza es crucial para una exploración dirigida y profunda del
conjunto de datos.
Agradezco
profundamente tu atención hasta este punto. Para explorar más a fondo, te
invito a acceder al cuaderno de Jupyter disponible en GitHub, donde se detalla
todo el análisis y el código en Python. No dudes en descargarlo, experimentar
con el análisis por ti mismo y compartir tus opiniones y sugerencias. ¡Tu
participación y feedback son muy valorados!
si quieres acceder al Notebook donde está todo el código y la explicación en Python 👇👽









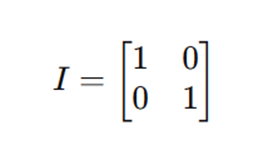

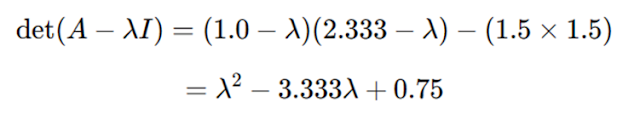









Comentarios
Publicar un comentario